PHI-S: Distribution Balancing for Label-Free Multi-Teacher Distillation
Mike Ranzinger, Jon Barker, Greg Heinrich, Pavlo Molchanov, Bryan Catanzaro, Andrew Tao
2024-10-03
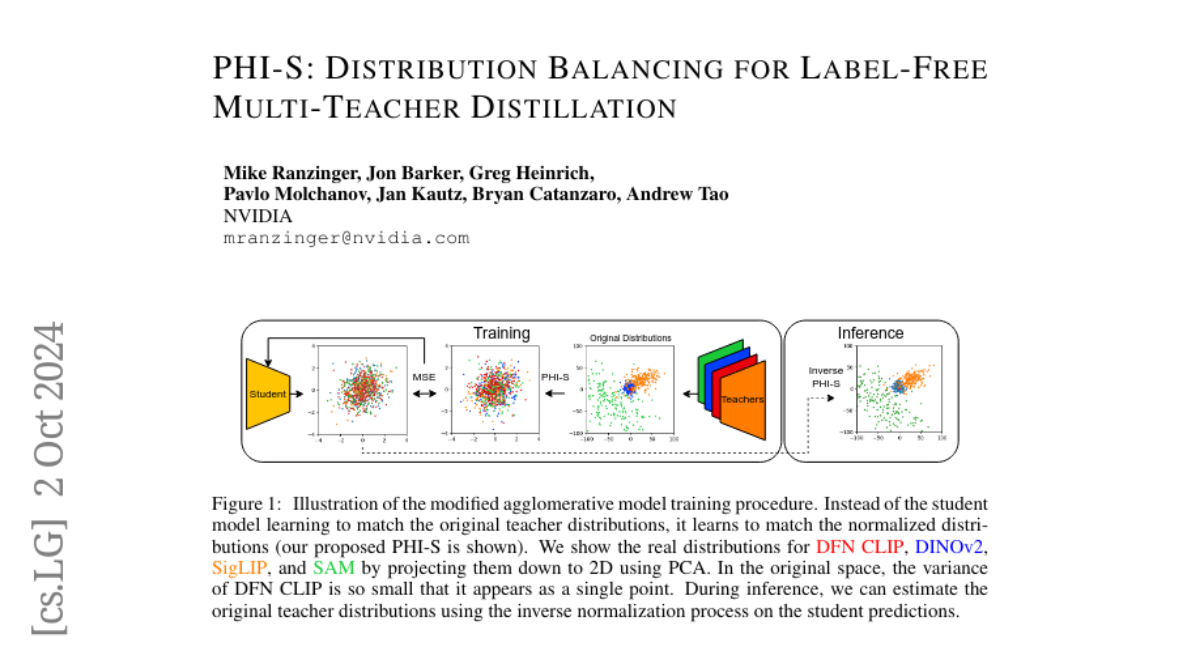
Summary
This paper discusses PHI-S, a new method for improving the performance of student models in machine learning by balancing the distribution of information received from multiple teacher models without requiring labels.
What's the problem?
In machine learning, especially in visual models, different teacher models have unique strengths and weaknesses. However, when these teachers provide knowledge to a student model, their varying ways of presenting information can lead to inconsistencies. This makes it difficult for the student model to learn effectively, especially when there are no labels to guide the learning process.
What's the solution?
PHI-S addresses this issue by using statistical normalization techniques to align the different distributions of information from the teacher models. It introduces a method called 'PHI Standardization,' which ensures that each part of the information is standardized using the same scale. This helps the student model learn more effectively from its teachers. The researchers tested this method and found that it produced better student models compared to other methods they studied.
Why it matters?
This research is important because it enhances how knowledge is transferred from multiple teacher models to a student model in machine learning. By improving this process, PHI-S can lead to better performance in various applications, such as image recognition and other tasks where understanding complex data is crucial.
Abstract
Various visual foundation models have distinct strengths and weaknesses, both of which can be improved through heterogeneous multi-teacher knowledge distillation without labels, termed "agglomerative models." We build upon this body of work by studying the effect of the teachers' activation statistics, particularly the impact of the loss function on the resulting student model quality. We explore a standard toolkit of statistical normalization techniques to better align the different distributions and assess their effects. Further, we examine the impact on downstream teacher-matching metrics, which motivates the use of Hadamard matrices. With these matrices, we demonstrate useful properties, showing how they can be used for isotropic standardization, where each dimension of a multivariate distribution is standardized using the same scale. We call this technique "PHI Standardization" (PHI-S) and empirically demonstrate that it produces the best student model across the suite of methods studied.